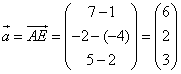Ortsvektoren und Repräsentanten

Grundsätzlich werden in der Vektorgeometrie zwei Arten von Vektoren unterschieden: Ortsvektoren und Repräsentanten!
Vektoren werden als Ortsvektoren bezeichnet, wenn ihre Anfangspunkte mit dem Koordinatenursprung übereinstimmen.
Das heißt, Ortsvektoren zeigen immer vom Punkt (0;0;0) auf einen Punkt im Raum!
Repräsentanten von Ortsvektoren können jedoch beliebig im Raum liegen. Ein Vektor ist also die unendliche (warum???) Menge aller Repräsentanten, die den selben Ortsvektor darstellen!

Um nun von beliebigen Vektoren (die durch Anfangs- und Endpunkt gegeben sind) den Ortsvektor zu bestimmen, den sie repräsentieren, muß man die Differenz der Koordinaten bilden. Man subtrahiert von den Koordinaten des Endpunktes die Koordinaten des Anfangspunktes: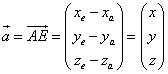

Im konkreten Fall sieht das dann so aus: Ein Vektor der vom Anfangspunkt A (1,-4,2) zum Endpunkt E (7,-2,5) verläuft, der repräsentiert den Ortsvektor vom Koordinatenursprung (0,0,0) zum Punkt (6,2,3).


Im Beispiel ist der Ortsvektor dargestellt. Darunter werden einige Repräsentanten dargestellt. Diese Repräsentanten haben alle dieselbe Richtung und denselben Betrag wie der Ortsvektor, aber ihr Anfangspunkt ist beliebig.

Hier sieht man einen Vektor. Da dieser Vektor im Koordinaten-Ursprung beginnt nennt man ihn Ortsvektor. Das bedeutet, er weist die Richtung vom Koordinaten-Ursprung zu einem Ort im Raum (KOS)!
   
Hier sieht man denselben Ortsvektor, aber nun mit einigen Repräsentanten. Man erkennt, dass alle Repräsentanten den gleichen Betrag und die gleichen Richtung haben, aber der Anfangspunkt variiert.

Wenn du nun noch ein paar Übungen selbst rechnen möchtest, dann klicke jetzt die
Übungsseite zu Ortsvektoren und Repräsentanten an!

[ Übungen ]   [ zurück zur Übersicht ]   [ Vektoraddition ]