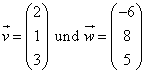Das Kreuzprodukt von Vektoren


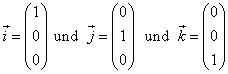Im Gegensatz zum Skalarprodukt, bei dem das Ergebnis ein Skalar ist, ist das Ergebnis des Kreuzproduktes ein Vektor. Beschäftigen wir uns also zuerst damit, wie man diesen Ergebnisvektor berechnet.

Wir nehmen wieder unsere bekannten Vektoren:
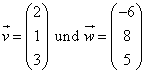Ferner benötigen wir die Einheitsvektoren in die einzelnen Koordinatenrichtungen: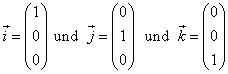
Mit diesen Voraussetzungen können wir nun folgende Matrix aufstellen:


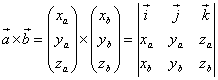
Aus dieser läßt sich (unter Abwandlung der Sarruschen Regel) die nachstehende Berechnung ausführen:


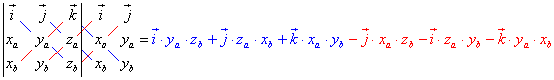
Da die Richtungsvektoren immer nur in eine Richtung des Koordinatensystemes weisen, kann man dieses Ergebnis auch als Vektor interpretieren. Nach dem Zusammenfassen ergibt sich also:


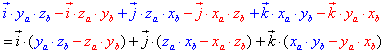
oder als Vektor:


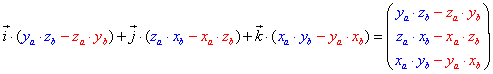
Dieser Vektor ist nun unser gesuchter Ergebnisvektor! Mit Zahlen sieht auch diese scheinbar umfangreiche Berechnung wieder einfacher aus. Sehen wir uns also nun das Kreuzprodukt unserer beiden Ausgangsvektoren an:


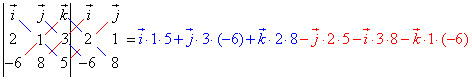
Dieser Term läßt sich auch wieder schön vereinfachen...


...und dann als Ergebnisvektor angeben:


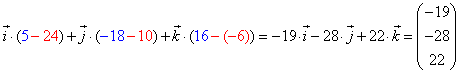
Das war also unser erstes Kreuzprodukt (ganz einfach mit Zahlen :-), aber wozu können wir dieses nun verwenden?! 
Dazu sollte man zuerst einmal wissen, das der Ergebnisvektor immer senkrecht auf den beiden Ausgangsvektoren steht und somit auch auf der Ebene, die durch diese beiden Vektoren aufgespannt wird. Also kann man das Kreuzprodukt verwenden, um Normalenvektoren (senkrecht stehende Vektoren) zu gegebenen Ebenen zu berechnen. 


Ausserdem gilt für das Ergebnis der Vektormultiplikation auch noch folgender Zusammenhang:
Zuerst sieht man die beiden ursprünglichen Vektoren (v-blau, w-hellblau):
   
Nun wird die Ebene, in der die beiden ursprünglichen Vektoren liegen, als Scheibe (ebenfalls rot) angezeigt:
   
Man kann erkennen, daß der Ergebnisvektor senkrecht auf dieser Ebene steht:
Kann man nun aber auch zeigen, daß dieser Ergebnisvektor wirklich senkrecht auf den beiden anderen Vektoren steht?
Ja, kann man!!! Nämlich mit dem Skalarprodukt. Das Skalarprodukt des Ergebnisvektores mit den beiden anderen Vektoren muß jeweils Null ergeben, damit der Kosinus des Winkels Null ist und somit der Winkel selbst 90 Grad beträgt. 

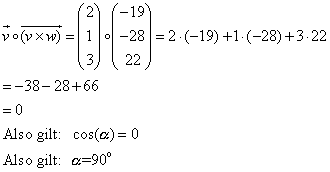
Tatsächlich steht also das Kreuzprodukt beider Vektoren senkrecht auf den beiden Vektoren und somit auch auf der Ebene, die durch die beiden Vektoren aufgespannt wird!

Mehr dazu in gibt es in den Übungen!

[ Übungen ]   [ zurück zur Übersicht ]   [ Spatprodukt ]